Multi-Head Latent Attention (MLA)详解

参考博客：

  • https://www.bilibili.com/video/BV1wjQvY6Enm

  • https://bruceyuan.com/post/hands-on-deepseek-mla-projection-absorption.html

  • https://kexue.fm/archives/10091

  • https://github.com/madsys-dev/deepseekv2-profile/blob/main/workspace/blog/optimizing-mla.md

1
2
3
4
洞见：
1.位置编码目前是添加到Q和K中，不再是直接添加到embedding中
2.RoPE虽然叫位置编码，但是自变量除了位置之外还有embeding维度。所以如果嵌入维度变了，位置编码也会变。
	所以可以只在固定维度添加位置编码？保证维度变了，位置编码不变？
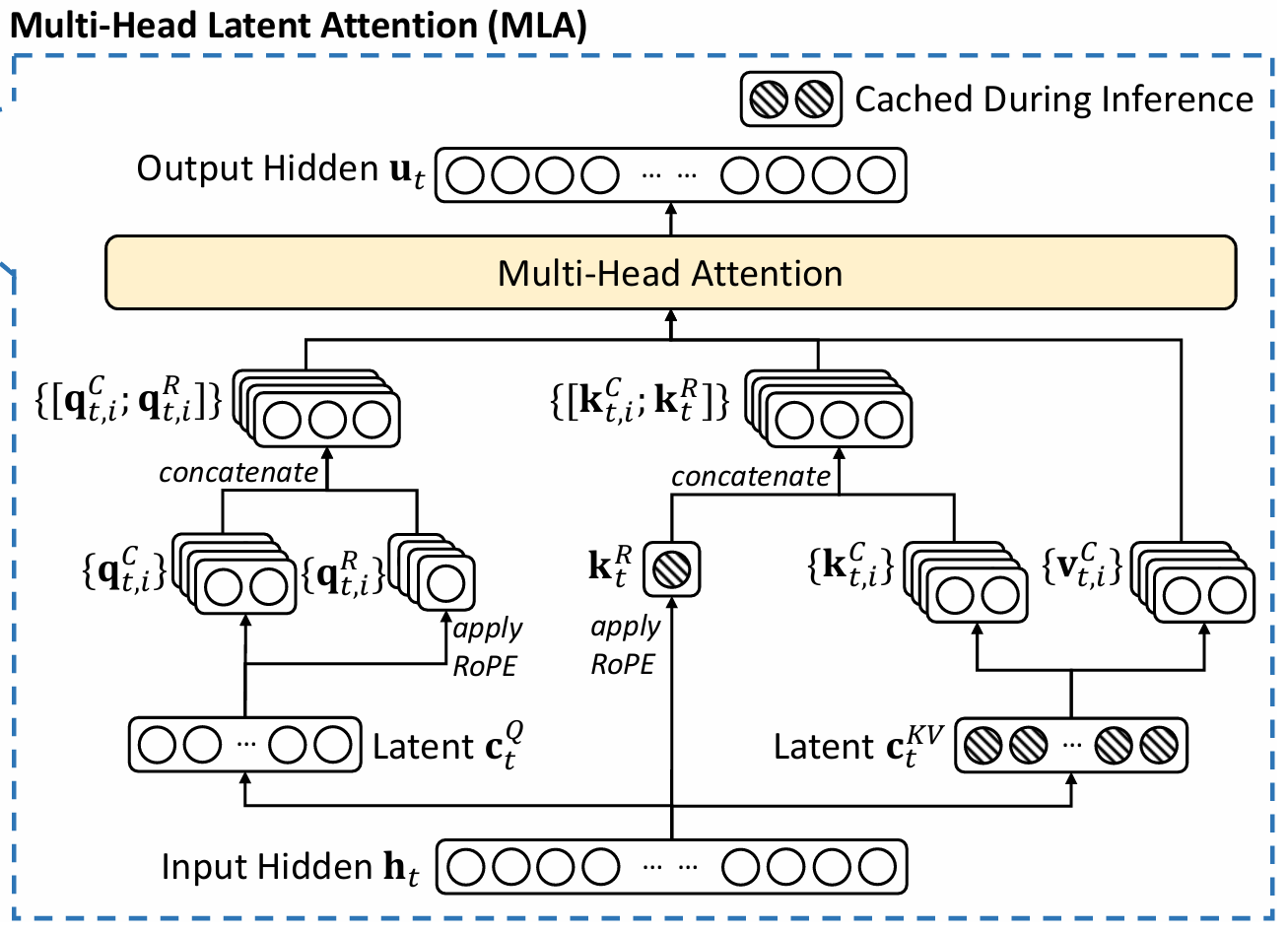
image-20250811164641624

1. Multi-Head Attention (MHA) 回顾

标准的多头注意力：d 表示嵌入维度，nh 表示注意力头的数量，dh 表示每个头的维度，ht ∈ Rd 表示在注意力层中第t个token的注意力输入。

标准MHA机制通过三个矩阵WQ、WK、WV ∈ ℝdhnh × d分别生成输入ht的查询向量qt ∈ ℝ𝑑ℎ、键向量kt ∈ ℝ𝑑ℎ和值向量vt ∈ ℝ𝑑ℎ。公式如下：

接下来，qt，kt，vt将被切分成nh个头，用于多头注意力计算:

其中： - qt, i, kt, i, vt, i ∈ ℝdh 是第 t 个 token 的第i个头的 query、key、value 向量。 - nh 是注意力头数，QKV分头前的特征维度为d，分头后每个头的维度是 dh。

公式含义：将原始的 qt, kt, vt 按列切分成 nh 个头的子向量。

每个头的注意力计算公式为:

最后拼接所有头的输出，再做输出投影:

其中 𝑊𝑂 ∈ ℝ𝑑 × 𝑑ℎ𝑛ℎ 是输出映射矩阵。

推理时问题：
- 所有 key 和 value 需要缓存，KV cache大小为 2𝑛ℎ𝑑ℎ𝑙（𝑙 为序列长度），当 batch size 和 𝑙 很大时会占用大量显存。

2. Low-Rank Key-Value Joint Compression（低秩 KV 联合压缩）

MLA 核心是通过低秩联合压缩减少 KV cache大小。

  1. 压缩输入:

    将输入 压缩到KV低维共享表示 $ c_t^{KV} ：$

    • 𝑐𝑡𝐾𝑉 ∈ ℝ𝑑𝑐：压缩后的 latent 表示，𝑑𝑐 ≪ 𝑑ℎ𝑛ℎ。
    • 𝑊𝐷𝐾𝑉 ∈ ℝ𝑑𝑐 × 𝑑：降维矩阵，D的含义是降维down_sample。

  2. 解码 key 和 value:

    从 𝑐𝑡𝐾𝑉 解码出 key 和 value： 𝑘𝑡𝐶 = 𝑊𝑈𝐾𝑐𝑡𝐾𝑉

    𝑣𝑡𝐶 = 𝑊𝑈𝑉𝑐𝑡𝐾𝑉

    • 𝑊𝑈𝐾, 𝑊𝑈𝑉 ∈ ℝ𝑑ℎ𝑛ℎ × 𝑑𝑐：升维矩阵，U的含义是升维up_sample。

  3. 低秩压缩后的注意力权重计算方式：

  1. 最后的输出:

多头注意力相当于把 注意力权重attention_weight从一维向量变为了二维向量，shape: (seq_len,) -> (seq_len, head_num)，但本质上还是一个张量，只是得到这个张量的方式注意力机制计算比较复杂。

优势：

  • 推理时仅需缓存 𝑐𝑡𝐾𝑉（每 token 只需 𝑑𝑐 维），KV 缓存大小从 2𝑑ℎ𝑛ℎ𝑙 缩减到 𝑑𝑐𝑙。
  • 可将 𝑊𝑈𝐾 ∈ ℝ𝑑ℎ𝑛ℎ × 𝑑𝑐 与 𝑊𝑄 ∈ ℝdhnh × d合并，将𝑊𝑈𝑉 ∈ ℝ𝑑ℎ𝑛ℎ × 𝑑𝑐 与 𝑊𝑂 ∈ ℝ𝑑 × 𝑑ℎ𝑛ℎ合并，无需显式生成或存储 key/value。

矩阵合并分析：

上面公式看似需要使用𝑐𝑡𝐾𝑉重新生成历史的KV，但是通过权重吸收(合并)可以将重新生成的步骤合并其他向量的投影中，从而无需真正重新生成。

𝑊𝑈𝐾 ∈ ℝ𝑑ℎ𝑛ℎ × 𝑑𝑐 与 𝑊𝑄 ∈ ℝdhnh × d的合并，维度变换是 d− > dhnh− > dc，吸收后是 d− > dc，如果是原始的MHA不进行维度压缩d− > dhnh，可以看出来吸收后相比MHA计算量减少，不吸收则增大计算量。

𝑊𝑈𝑉 ∈ ℝ𝑑ℎ𝑛ℎ × 𝑑𝑐 与 𝑊𝑂 ∈ ℝ𝑑 × 𝑑ℎ𝑛ℎ合并，维度变换是 dc− > dhnh− > d, 吸收后是dc− > d，同样吸收后相比MHA计算量减少，不吸收则增大计算量。

3. Low-Rank Query Compression（低秩 Query 压缩）

虽然压缩 Query 不能减少 KV 缓存，但是也能节省计算。

  1. 压缩 Query：
    𝑐𝑡𝑄 = 𝑊𝐷𝑄ℎ𝑡   𝑞𝑡𝐶 = 𝑊𝑈𝑄𝑐𝑡𝑄  
    • 𝑐𝑡𝑄 ∈ ℝ𝑑𝑐′：压缩后的 query 表示，𝑑𝑐′ ≪ 𝑑ℎ𝑛ℎ。
    • 𝑊𝐷𝑄 ∈ ℝ𝑑𝑐′ × 𝑑，𝑊𝑈𝑄 ∈ ℝ𝑑ℎ𝑛ℎ × 𝑑𝑐′：降维和升维矩阵。

作用：

  • 降维后再升维，减少全连接计算量，尤其适用于输入维度 𝑑 较大的场景。

4. Decoupled Rotary Position Embedding（解耦 RoPE）

背景

前面的推理没有考虑位置编码，如果考虑RoPE位置编码，会发现权重吸收和位置编码不兼容： 𝑞𝑡⊤𝑘j𝐶 =  > RoPE(𝑞𝑡⊤)RoPE(𝑘j𝐶)

前面 𝑊𝑈𝐾 与 𝑊𝑄 可以合并，是因为$(WQ)𝑊^{𝑈𝐾} 是常量，但是(WQ)R_{j-t} 𝑊^{𝑈𝐾}是与query向量的位置t相关的变量R_{j-t}$，即随推理过程中query的位置变化而变化，导致旧的缓存不能直接使用，所以无法直接合并。

为什么GQA的低秩投影没有受RoPE影响，因为GQA只减少了头数，计算时又恢复了头数，但是隐式恢复头数直接通过广播实现，不涉及特征维度改变序列长度改变；而MLA减小的是每个头的特征维度，计算时为了避免增加计算量，只能隐式恢复特征维度，即需要借助权重吸收，而两个权重之间又夹着RoPE，没办法权重吸收。

RoPE（Rotary Position Embedding）对 key 和 query 都是位置敏感的。

若直接将 RoPE 应用于压缩后的 key，升维矩阵 𝑊𝑈𝐾 无法与 𝑊𝑄 合并，影响推理效率？

一个简单的逻辑应该是把位置编码都应用到压缩后的特征上。

原因

  • RoPE 是依赖位置的旋转矩阵，矩阵乘法不满足交换律。
  • 若在升维后的 key 上应用 RoPE，需重新计算所有历史 key 的位置编码，无法仅用缓存恢复。

解决方案

将 query 和 key 分为两部分，一部分就用MLA不使用RoPE 位置编码，另一部分用MQA使用位置编码：

  1. 对 query 和 key 分别应用 RoPE：

    将输入的查询内容向量 ctQ通过矩阵 WQR投影到 RoPE 编码后的空间，得到分离后的旋转位置编码查询向量 qtR，并按多头nh分块。 [𝑞𝑡, 1𝑅; 𝑞𝑡, 2𝑅; …; 𝑞𝑡, 𝑛ℎ𝑅] = RoPE(𝑊𝑄𝑅𝑐𝑡𝑄)  (14) 将隐藏状态 通过矩阵 WKR投影，并应用 RoPE 得到分离后的旋转位置编码键向量$ k^R_t 。$

  2. 拼接压缩部分和 RoPE 部分：

    将内容查询向量与旋转位置编码查询向量进行拼接，得到最终的第 i个头的查询向量。 𝑞𝑡, 𝑖 = [𝑞𝑡, 𝑖𝐶, 𝑞𝑡, 𝑖𝑅]  (16) 将内容键向量与旋转位置编码键向量拼接，得到最终的第i个头的键向量。 𝑘𝑡, 𝑖 = [𝑘𝑡, 𝑖𝐶, 𝑘𝑡, 𝑖𝑅]  (17)

  3. 注意力计算：

    通过点积计算第 i 个头在时间步 t的查询向量与历史键向量的相关性，除以 进行缩放，然后使用 Softmax 得到注意力权重，对对应的值向量 vj, iC进行加权求和。

  4. 最终输出：

    将所有头的输出 ot, i 拼接起来，并通过输出权重矩阵 WO得到最终的输出向量 ut。 𝑢𝑡 = 𝑊𝑂[𝑜𝑡, 1; 𝑜𝑡, 2; …; 𝑜𝑡, 𝑛ℎ]  (19)

其中 WQR ∈ ℝdhRnh × dc′ 和$ W^{KR} {dR_h d}是分别用于生成分离查询向量和分离键向量的矩阵；RoPE(·)表示应用旋转位置编码的操作；符号[;]$表示拼接操作。在推理阶段，分离的键向量也需要被缓存。因此，MLA需要一个包含 (dc + dhR)l元素的 KV 缓存。

参数说明：

  • dhR: RoPE 部分的维度。
  • 推理时只需缓存 ctKV（大小约为 𝑑𝑐 + 𝑑ℎ𝑅）。

5. 总结 MLA 思路

MLA 的核心目标是降低推理时的显存占用和计算延迟，同时保持注意力效果。具体方法包括：
1. 低秩联合压缩 KV：通过共享压缩表示 𝑐𝑡𝐾𝑉 减少 KV 缓存大小。
2. 低秩 Query 压缩：减少 Query 的计算量。
3. 解耦 RoPE：在保留位置编码效果的同时，使压缩策略兼容 RoPE，避免破坏缓存复用。

最终效果：
- 显存占用从 2𝑑ℎ𝑛ℎ𝑙 降至 𝑑𝑐𝑙。
- 计算效率提升，适用于大规模模型部署。